Vectores en R3 

1.- ¿Que es adición de vectores en R3? Gráfica.

Para realizar la suma matemática de vectores, lo único que tenemos que hacer es sumar las respectivas componentes de los vectores sumándolos, así obtenemos el vector suma.

EJEMPLO:

Obtener la suma de los vectores A(-5, 2, 3) y D(2, 3, -1) con modulo resultante.
Hacemos la grafica primero, dándole valores a los puntos con i, j, k por ejemplo…
A = -5i + 2j + 3k
B = 2i + 3j -1k

  

 2.- ¿Cómo se representa geométricamente un vector suma o resta en un sistema de coordenadas?

  Para graficar geometricamente un vector en R3 se deben realizar dos metodos:

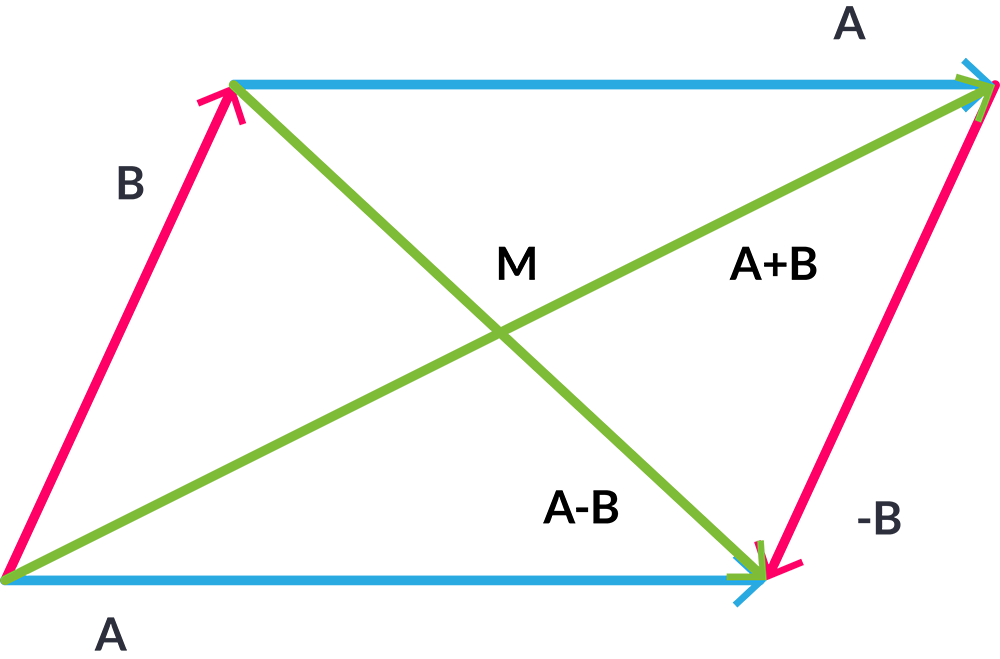
Paralelogramo:

Consiste en colocar los 2 Vectores en el mismo punto de origen, y de allí, luego de realizar la operación (suma o resta), se construye un paralelogramo, usando como lados los 2 vectores. En el caso de la suma, el vector resultante se representaría desde el punto de origen hasta el vértice contrario del paralelogramo.

Poligonal:

   Consiste en dibujar un vector seguido de otro, este se puede realizar muchas veces sin dificultad o problema alguno, es decir, sirve para sumar un número grande de vectores.

 3.- ¿Qué es sustracción de Vectores? Gráfica.
  

La sustraccion de Vectores es cuando se resta sus componentes, para realizar la resta de Vectores en R3 son los mismos pasos de la adicion de Vectores en R3 distinto a que el segundo vector se le invertira su signo.

V1(1,-5,4) - V2(3,6,-7)= V(1-3,-5-6,4-(-7).

V(-2,-11,11)

4.- ¿Cómo calcular la dirección y sentido de un vector en R3?

La dirección de un Vector se calcula usando un mecanismo llamado "Cosenos Directores". A traves de un procedimiento basico matematico ver el angulo de cada uno de ellos.

Con X, Alpha = ArcCos (X/Magnitud del vector)
Con Y, Beta = ArcCos (Y/Magnitud del vector)
Con Z, Gamma = ArcCos (Z/Magnitud del vector)

El sentido de un vector se calcula como la raiz cuadrada de la suma del cuadrado de todas sus componentes.

Tutorial, adición y sustracción de vectores en R3